trigonometry Proving trig identity $\tan (2x)−\tan (x)=\frac {\tan (x)} {\cos (2x)}$ Mathematics Stack ExchangeCos 2x is an important identity in trigonometry which can be expressed in different ways It can be expressed in terms of different trigonometric functions such as sine, cosine, and tangentCos 2x is one of the double angle trigonometric identities as the angle in consideration is a multiple of 2, that is, the double of xStepbystep Solution Problem to solve s i n 2 x − t a n x = t a n x c o s 2 x sin2xtanx=tanxcos2x sin2x−tanx = tanxcos2x Choose the solving method Prove from LHS Prove from RHS Express everything into Sine and Cosine Learn how to solve trigonometric identities problems step by step online $\sin\left (2x\right)\frac {\sin\left (x

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Homeworklib
Tan(x/2) identity proof
Tan(x/2) identity proof-Proof Half Angle Formula tan (x/2) Product to Sum Formula 1 Product to Sum Formula 2 Sum to Product Formula 1 Sum to Product Formula 2 Write sin (2x)cos3x as a Sum Write cos4xcos6x as a Product Prove cos^4 (x)sin^4 (x)=cos2x Prove sinxsin (5x)/ cosxcos (5x)=tan3xQuestion Prove each identity tan^2x sin^2x = tan^2xsin^2x Answer by greenestamps(9774) (Show Source) You can put this solution on YOUR website!



3
tan x = n tan y, sin x = m sin y then prove that m^2/n^21 = cos^2x trig Prove the identity sin(3 pi /2 x) sin(3pi/2 x) = 2cosx Maths complex numbers Find tan(3 theta) in terms of tan theta Use the formula tan (a b) = (tan a tan b)/1 tan a tan b) in two stepsWe can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 xAnswer to Prove the identity {1 tan^2 x} / {sin^2 x cos^2x} = sec^2 x By signing up, you'll get thousands of stepbystep solutions to your
Now apply identity tan (ab)= (tan a tan b)/ (1tan atan b) tan2x can be solved by this method then by doing Tan (xx) and you will get tan2x=2tanx/ (1 tanxsquare) Tan3x=3tanx cube of tanx/1–3*square if tanx 7K views View upvotes ·We will use the following trigonometric formula to prove the formula for tan 2x tan (a b) = (tan a tan b)/ (1 tan a tan b) We have tan 2x = tan (x x) = (tan x tan x)/ (1 tan x tan x) = 2 tan x/ (1 tan 2 x) Hence, we have derived the tan 2x formula using theA number of basic identities follow from the sum formulas for sine,cosine,and tangent The first category of identities involves doubleangle formulas Section 53 Group Exercise y = sin 2x 0, 2p, q by −3, 3, 1 sin 2x Z 2 sin x y = 2 sin x y = sin 2x tan 2u = 2 tan u We can prove the first two formulas in the box by working with
Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity Answer linkGeneral Tan of Sum formula Now, let x=tan (A) and y=tan (B), so arctan (x)=A and arctan (y)=B, and then take the arctan of both sides, giving you So the lefthandside of the identity to be proven is The sum of arctans of reciprocals is pi/2, proving the identity




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube
To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x The preceding three examples verify three formulas known as the reductionI need to prove this identity tan^2xsin^2x = tan^2xsin^2x start with left side tan^2xsin^2x =(sin^2x/cos^2x)sin^2xThese identities are useful whenever expressions involving trigonometric functions need to be simplified An important application is the integration of nontrigonometric functions a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Trig Identity Sec2x Minus Tan2x T10 Youtube
Prove each identity a) 1cos^2x=tan^2xcos^2x b) cos^2x 2sin^2x1 = sin^2x I also tried a question on my own tan^2x = (1 – cos^2x)/cos^2x RS= sin^2x/cos^2x I know that the Pythagorean for that is sin^2x cos^2x That's all I could do Calculus Okay so I have a question on my assignment that says You are given that tan(y) = xTrigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation Trigonometric Identities are true for every value of variables occurring on both sides of an equation Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles Sine, cosine and tangent are the primaryNow divide numerator and denominator by cosAcosB to obtain the identity we wanted tan(AB) = tanAtanB 1−tanAtanB (16) We can get the identity for tan(A − B) by replacing B in (16) by −B and noting that tangent is an odd function tan(A−B) = tanA−tanB 1tanAtanB (17) 8 Summary There are many other identities that can be generated



1



What Is The Formula Of Tan2x Quora
Prove the trigonometric identity tan^2 (x)1=sec^2 (x) We can start with the identity sin 2 (x)cos 2 (x)=1 If we divide through the equation by cos 2 (x), we get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) If we look at the left hand side of the equation sin 2 (x)/cos 2 (x) is equal to tan 2 (x), and cos 2 (x)/cos 2 (x) is equalProve tan^2 (x)sin^2 (x)=tan^2 (x)sin^2 (x) Trigonometric Identities Solver Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to SumTrigonometric identities Intro to Pythagorean trigonometric identities Converting between trigonometric ratios example write all ratios in terms of sine Practice Evaluating expressions using basic trigonometric identities Trigonometric identity example proof involving sec, sin, and cos



Trig Identities Prove Cot X Tan X 2tan 2x Physics Forums



What Is Integral Of Sin2x Tan2x Quora
Use the double angle formulas to prove the identity csc 2 θ − cot 2 θ = tan θ \csc 2\theta \cot 2\theta = \tan \theta csc2θ−cot2θ = tanθ We have csc 2 θ − cot 2 θ = 1 sin 2 θ − cos 2 θ sin 2 θ = 1 − cos 2 θ sin 2 θProve sec^2xtan^2x=1 Trigonometric Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to Sum\tan \cot \csc \sec \alpha \beta \gamma \delta \zeta \eta \theta \iota \kappa \lambda \mu identity\\sin(2x) identity\\cos(2x) trigonometricidentitycalculator prove tan2x2tan2xsin^{2}x= sin2x he Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions ) If you've ever taken a ferris wheel ride then you




Tangent Half Angle Formula Wikipedia




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
To derive c), divide by y2 Or, we can derive both b) and c) from a) by dividing it first by cos 2θ and then by sin 2θ On dividing line 2) by cos 2θ, we have 1 tan 2θ = sec 2θ 1 cot 2θ = csc 2θ The three Pythagorean identities are thus equivalent to one another ProofTrigonometricidentitycalculator Prove tan^{2}(x) (1cot^{2}x) = sec^{2}x ar Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions )• To obtain halfangle identity for tangent, we use the quotient identity and the half angle formulas for both cosine and sine tan x/2 = (sin x/2)/ (cos x/2) (quotient identity)



7 Proving Ids Trig Functions Identities




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
It is proved the tan of sum of two angles is equal to the quotient of sum of tangents of both angles by the subtraction of products of tangents of both angles from one The expansion of tan of sum of two angles is called as angle sum identity for the tan function and also called as tan of compound angle identity Proof We will apply the following more fundamental trigonometric identities csc x = 1 sin x ( Reciprocal Identity) cos 2 x sin 2 x = 1 ( Pythagorean Identity) The proof is started from the lefthand side sin A csc A − sin 2 A = sin A ⋅ 1 sin A − sin 2 A = 1 − sin 2 A = cos 2 A Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes
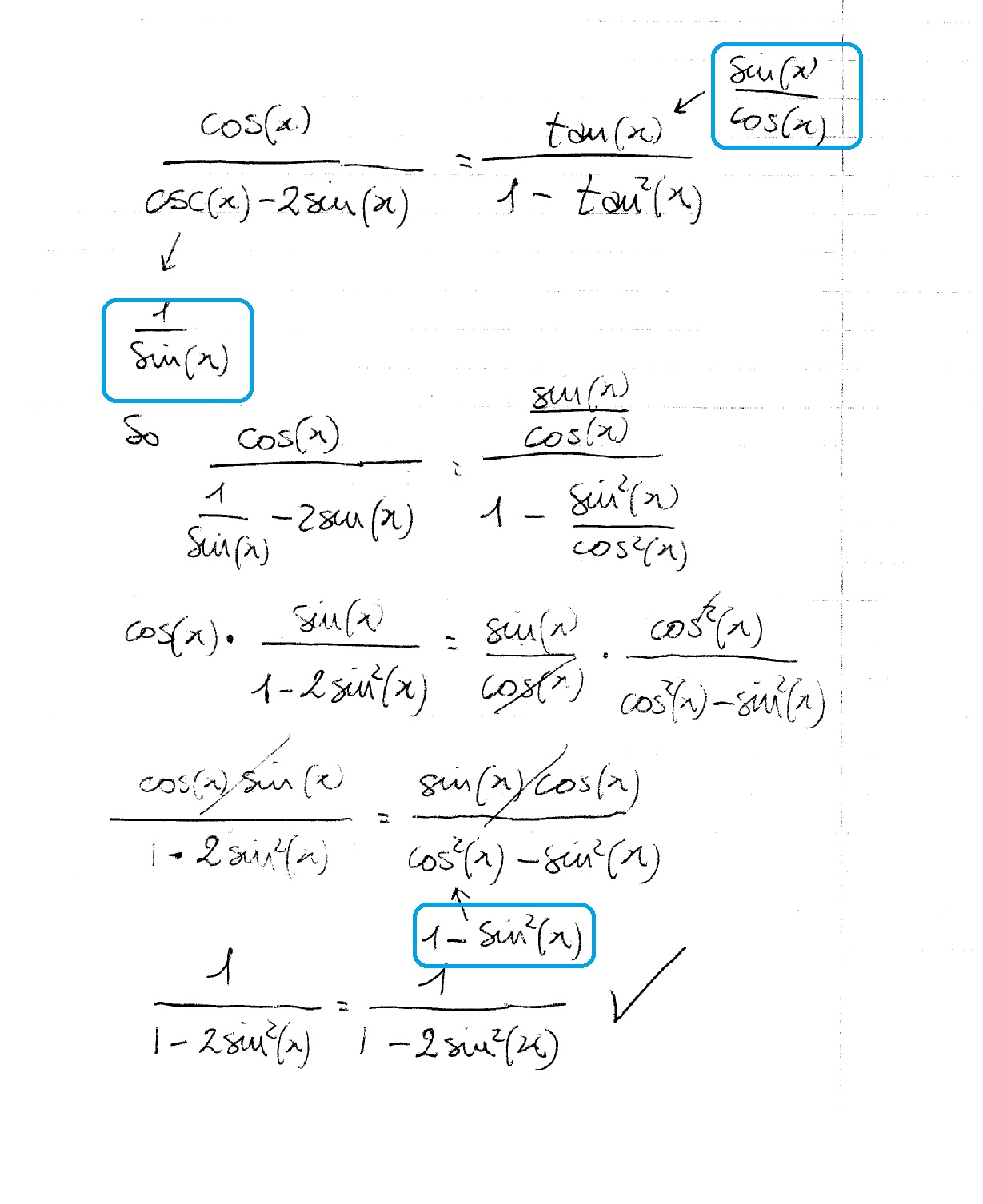



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic
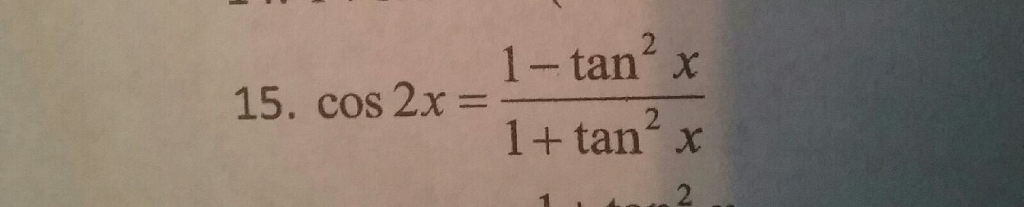



Solved Prove The Identity Cos 2x 1 Tan 2 X 1 Tan 2 X Chegg Com
The inverse trigonometric functions are also called arcus functions or anti trigonometric functions These are the inverse functions of the trigonometric functions with suitably restricted domainsSpecifically, they are the inverse functions of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometricTan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2 (cos (x))^2 – 1 Proof 77K views View upvotes ·The subtraction of the tan squared of angle from secant squared of angle is equal to one and it is called as the Pythagorean identity of secant and tangent functions $\sec^2{\theta}\tan^2{\theta} \,=\, 1$ Popular forms The Pythagorean identity of secant and tan functions can also be written popularly in two other forms $\sec^2{x}\tan^2{x} \,=\, 1$
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



3
Question I need to prove this identity tan^2xsin^2x = tan^2xsin^2x Answer by lwsshak3() (Show Source) You can put this solution on YOUR website! In this video, we are going to derive the identity for the tangent of 2xThe identity for tan(x y) has been explained in the following videohttps//youtubList of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) andcos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ andcos θ The tangent (tan) of an angle is the ratio of the sine to the cosine
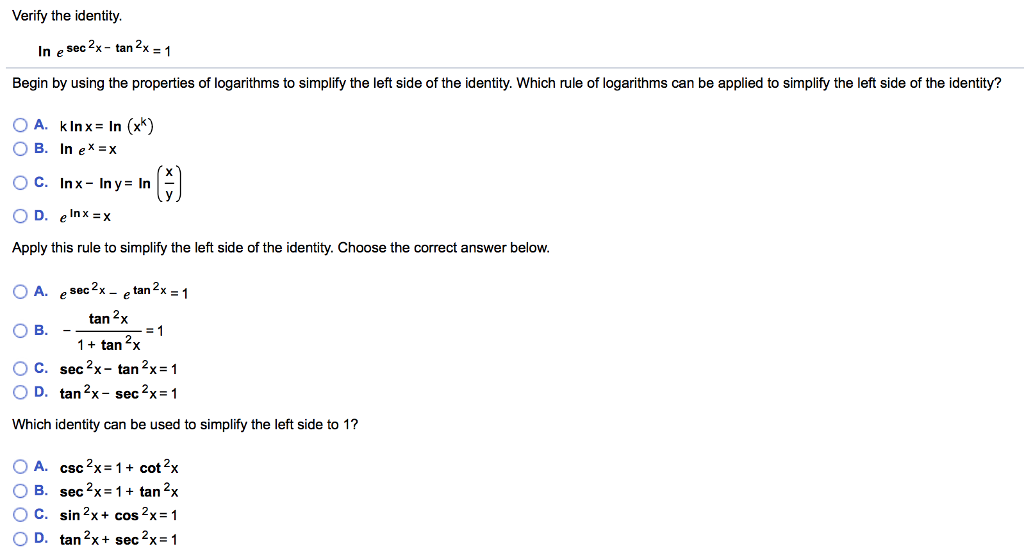



上 Tan2x Identity ただの悪魔の画像
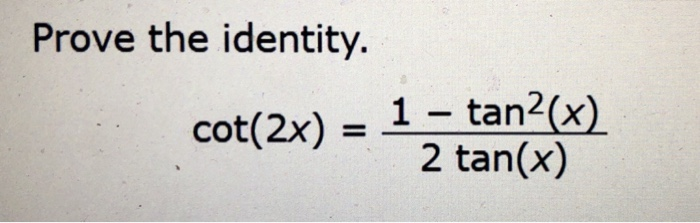



Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com
In this video, we are going to derive the identity for the tangent of 3xThe identity tan(2x) has been explained in the following videohttps//youtube/IcU_mSo sec^2 (x)=1tan^2 (x) This is one of the three Pythagorean identities in trigonometry, but if you don't recognize it, try converting to sines and cosines 1/cos^2 (x)=1sin^2 (x)/cos^2 (x) Now, multiply each term by cos^2 (x) to get 1=cos^2 (x) sin^2 (xAnswer to Solved Prove the identity 1 cos(2x)/sin(2x) = tan(x) 1



How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




Solved Using Standard Trigonometric Identities Show That Chegg Com
We have to prove that (tan x)^2 (sin x)^2 = (tan x)^2 * (sin x)^2 Start from the left hand side (tan x)^2 (sin x)^2 use tan x = sin x / cos x (sin x)^2/(cos x)^2 (sin x)^2To derive b), divide line (1) by x2;The more important identities You don't have to know all the identities off the top of your head But these you should Defining relations for tangent, cotangent, secant, and cosecant in terms of sine and cosine The Pythagorean formula for sines and cosines This is probably the most important trig identity
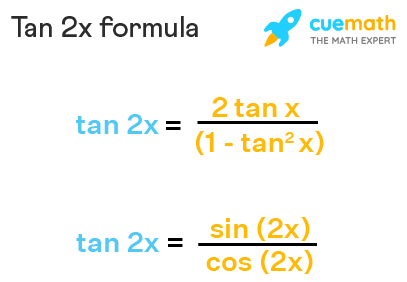



Tan 2x Formula What Is Tan 2x Formula Examples




Solved Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com
Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be usedFor a proof like this, I like to start with the more difficultlooking side, and aim to end up with the expression on the other side Starting with the left hand side, the first thing to change is the sin2x, because the expression on the RHS only has terms of x, not 2xUsing the identity sin2x = 2sinxcosx, the expression becomes 2sinxcosx/(1 (tan 2 x))Next, we will change the tan 2 x to




Solved 4 Prove The Following Trigonometric Identity Chegg Com




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




70pmylqshcbm




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
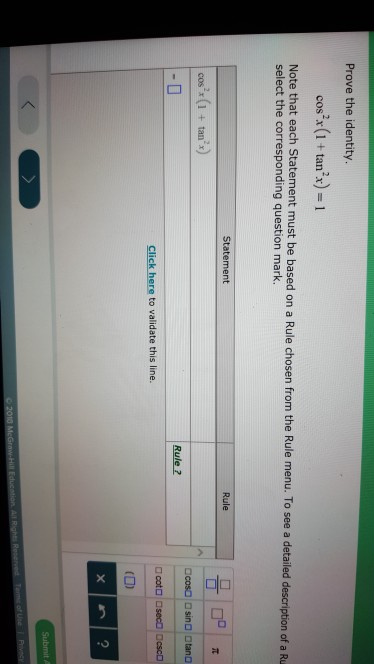



Solved Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube




Integrate Sec 2x Method 1




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
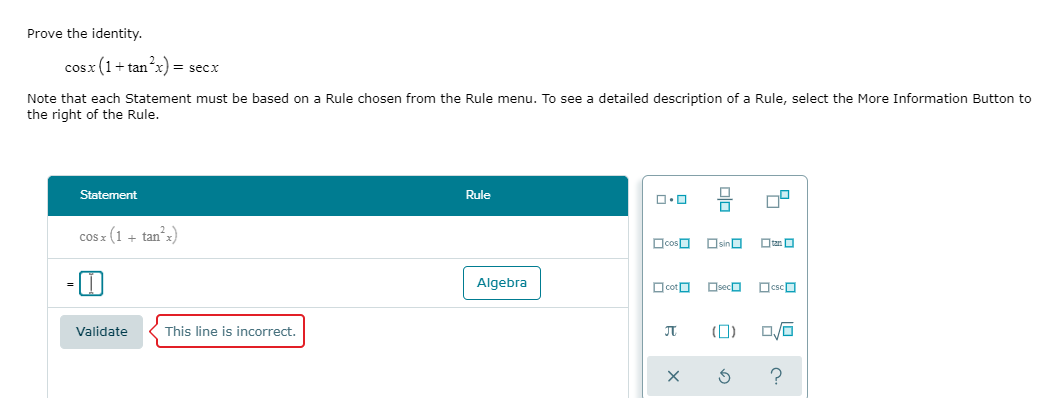



Solved Prove The Identity Cosx 1 Tan2x Secx Note That Chegg Com




bestpictjcry Tan 2x Tan 2x




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



Tan2x 1 ただの悪魔の画像



What Is The Formula Of Tan2x Quora
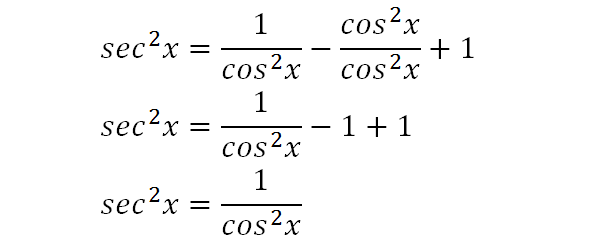



Integrate Sec 2x Method 2




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Tan 2x Formula What Is Tan 2x Formula Examples
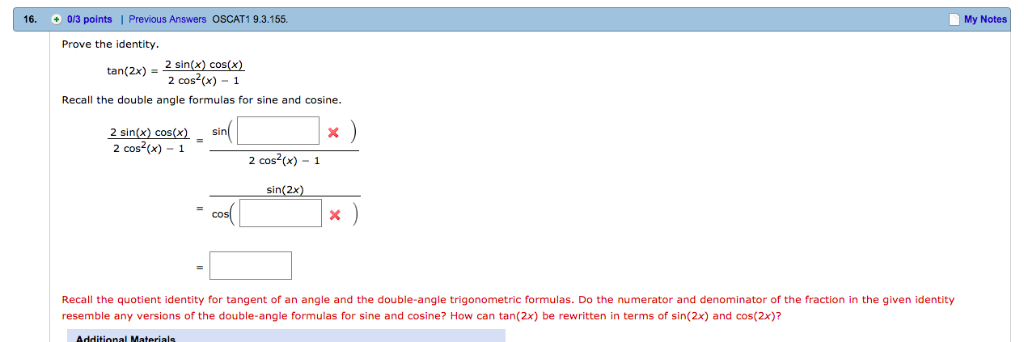



Solved 16 0 3 Points Previous Answers Oscat1 9 3 155 My Chegg Com




How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic



How To Prove Cot X Tan X 2cosec 2x Cos 2x Quora



1




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com
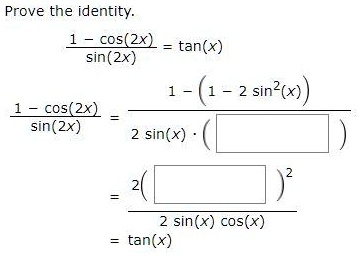



Solved Prove The Identity Cos 2x Tan X Sin 2x 1 1 2 Sin X Cos 2x Sin 2x 2 Sin X 2 Sin X Cos X Tan X
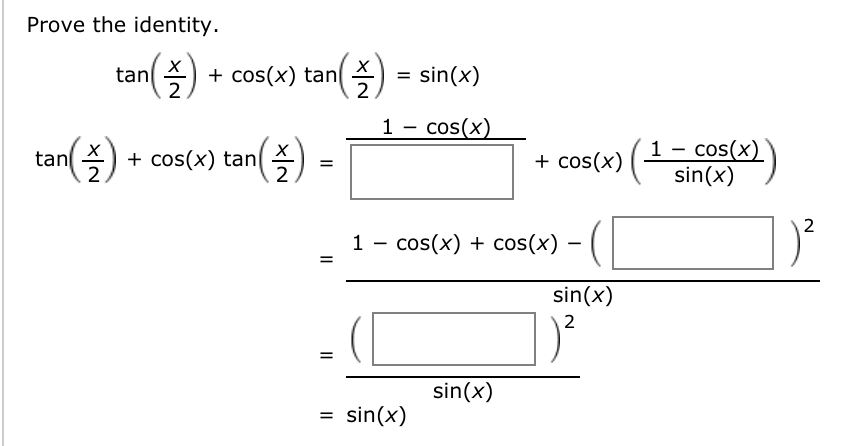



Solved Prove The Identity Cot 2x 1 Tan2x 2 Tan X Chegg Com



3




Tan2x Sec2x ただの悪魔の画像



Solved Prove Trigonometric Identities Course Hero




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download




How Many Can You Derive From First Principles Ppt Download



Prove Sin2x 2tanx 1 Tan 2x Socratic




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




How Many Can You Derive From First Principles Ppt Download
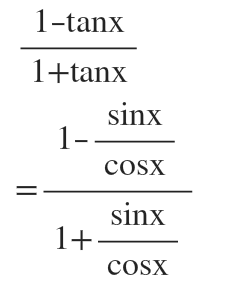



Answered Prove The Following Identity 1 Tan X Bartleby



bestpictjcry Tan 2x Tan 2x




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
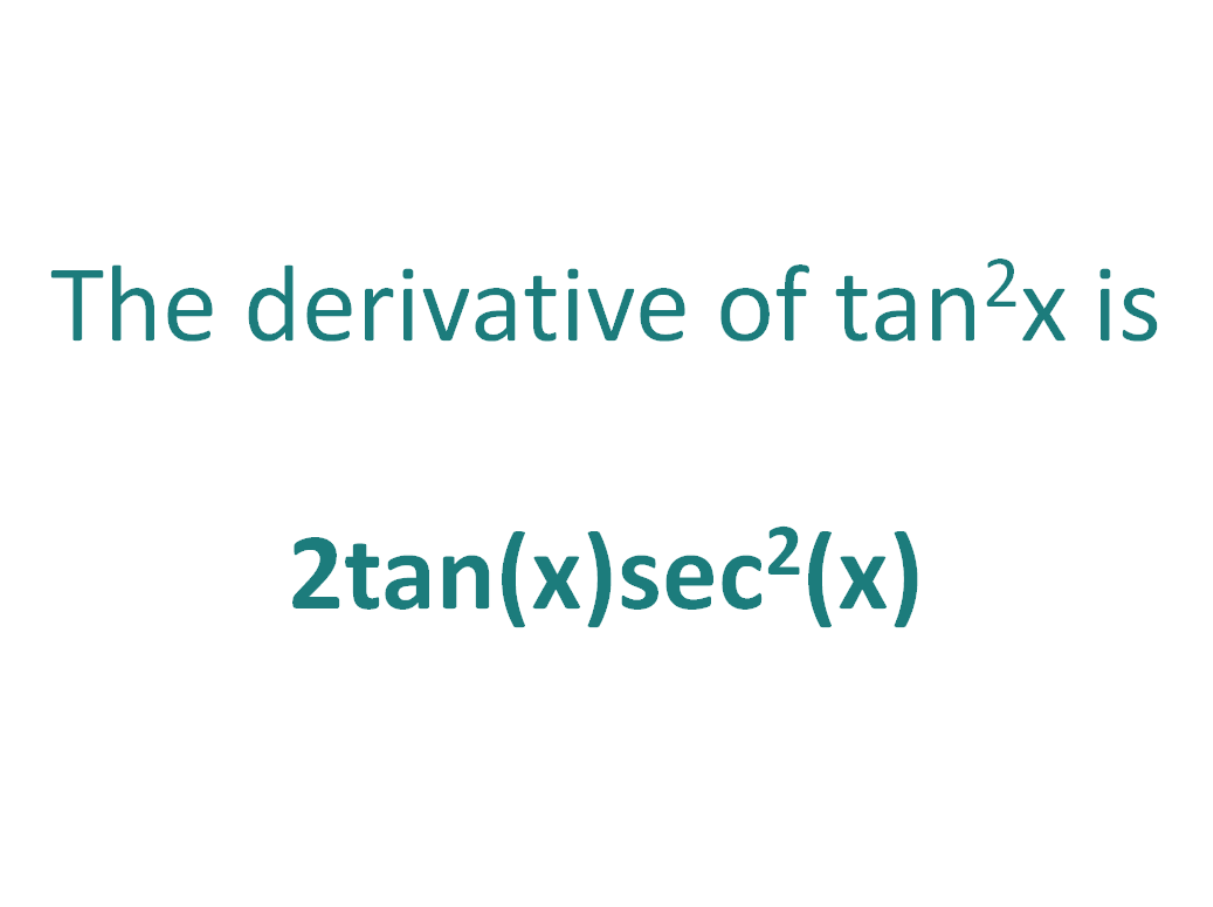



The Derivative Of Tan 2x Derivativeit



What Is The Formula Of Tan2x Quora




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube



What Is The Formula Of Tan2x Quora



Answered Trigonometric Identities And Equations Bartleby
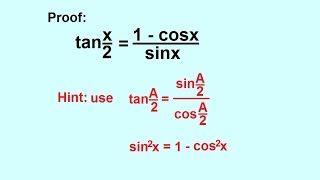



Lecture 129 Proof Half Angle Formula Tan X 2 Cosmolearning Mathematics




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Homeworklib



bestpictjcry Tan 2x Tan 2x




上 Tan2x Identity ただの悪魔の画像




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Which Identity Needs To Be Used To Prove Tan Pi 2 X Cot X Brainly Com
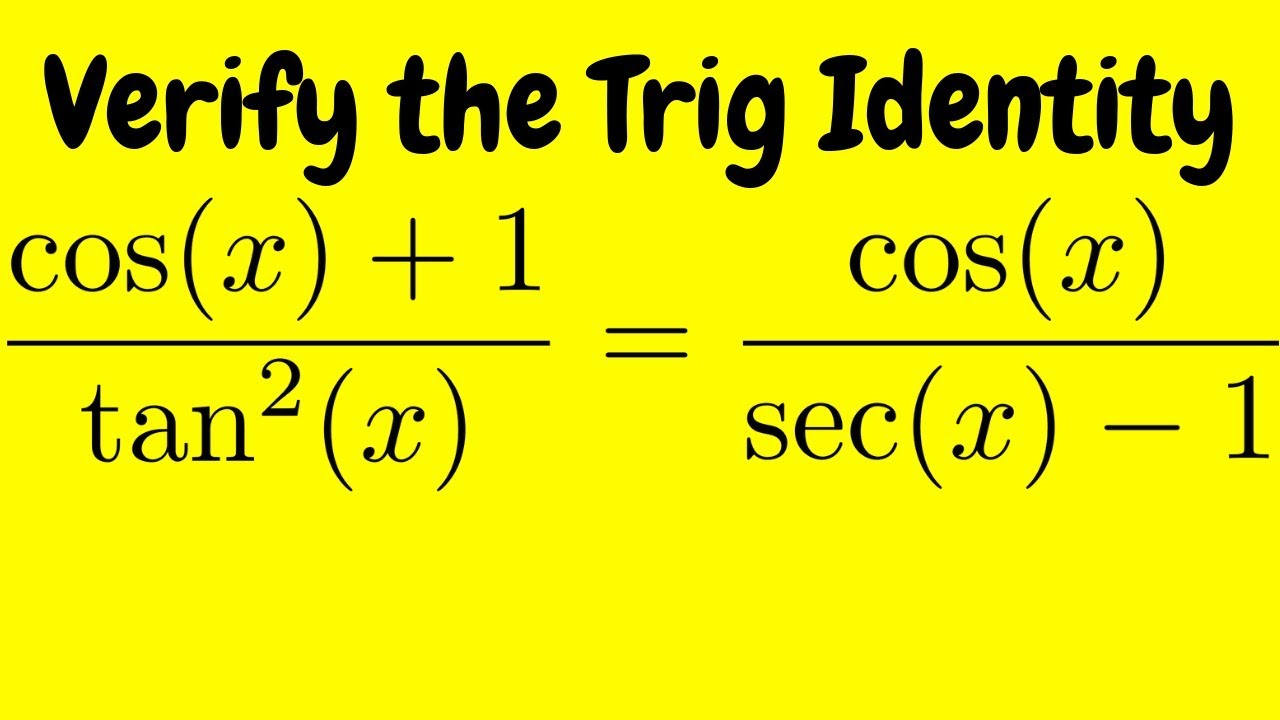



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Proof Tan 2 1 Sec 2 Youtube
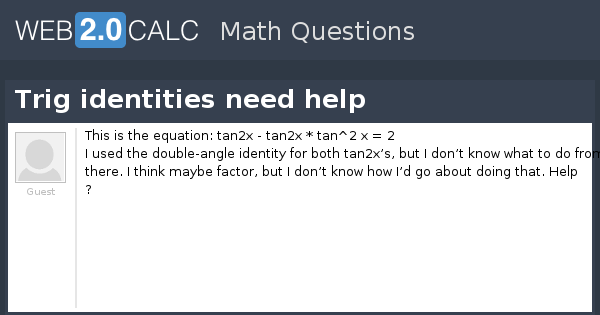



View Question Trig Identities Need Help




How Many Can You Derive From First Principles Ppt Download




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



A Trig Identity




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




Show That Tan 3xtan 2xtan X Tan 3x Tan 2x Tan X Orprove That Cos 2x Cos 2left X Frac Pi 3right Cos 2left X Frac Pi 3right Frac 3 2 Snapsolve




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



What Is The Formula Of Tan2x Quora



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero



Solved Prove The Following Trig Identities Course Hero




Solved Prove Or Disprove The Given Identity Sec 2 X Chegg Com




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
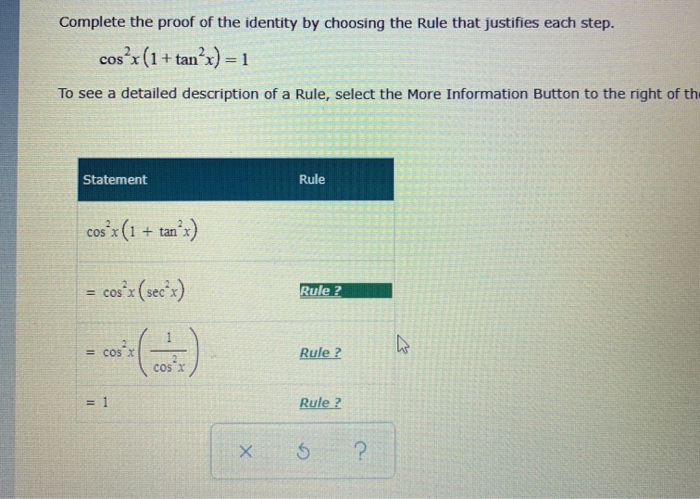



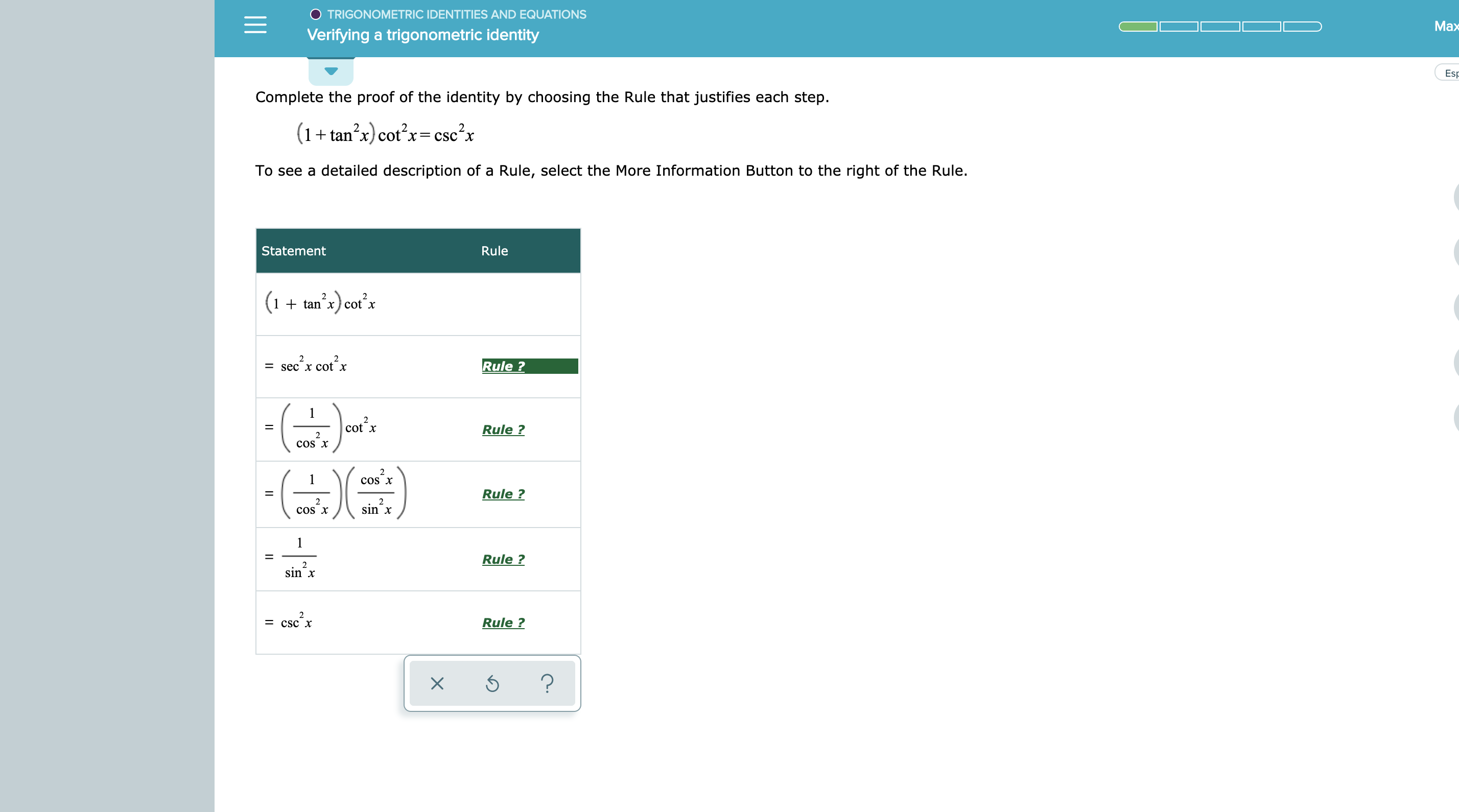
Solved Complete The Proof Of The Identity By Choosing The Chegg Com




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube



Q35 A Prove That Tex Frac Tan 2x Tan X Tan 2x Tan X Sin 2x Tex Snapsolve
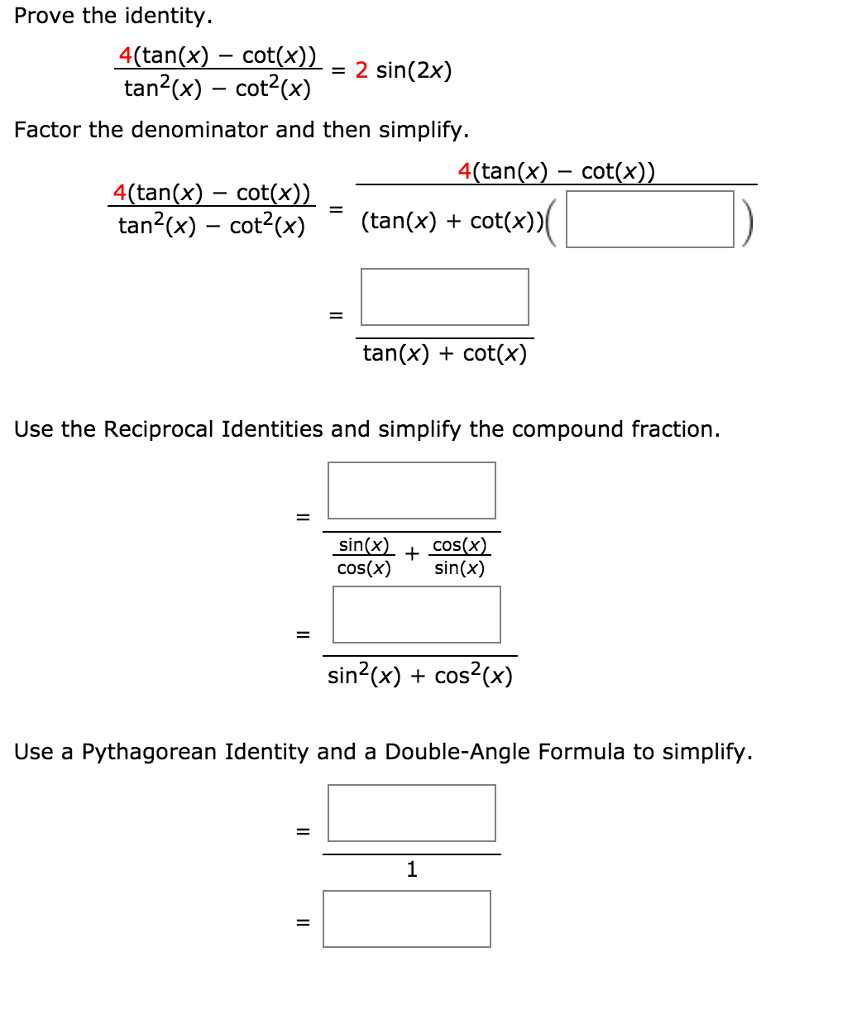



Solved Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com




9 1 Identities And Proofs Ppt Download



How To Prove The Identity Tan2 X Sin2 X Tan2 X Sin2 X Quora




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




Solved Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com



Tan2x 1 ただの悪魔の画像



Bestmaths Online Proof 4




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Analytic Trig Ppt Video Online Download
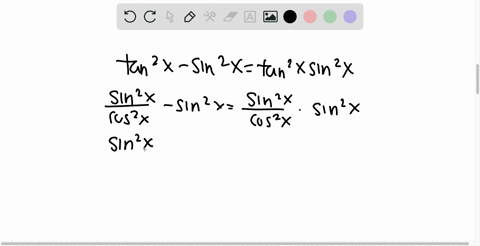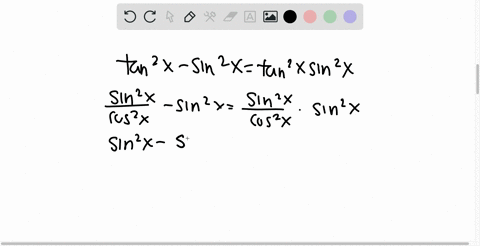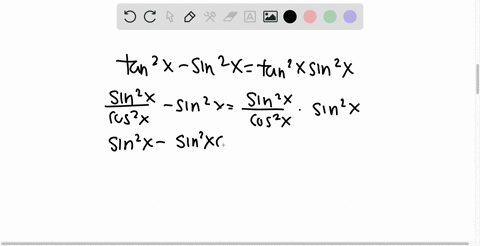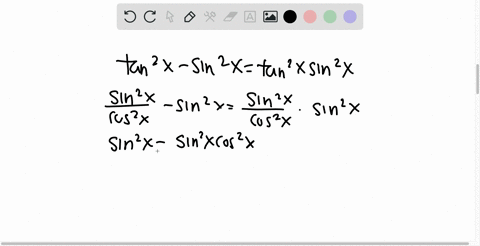



Solved Prove Each Identity Frac Tan 2 X Tan X Tan 2 X Tan X Sin 2 X



0 件のコメント:
コメントを投稿